Home » Assignments

Category Archives: Assignments

COVID-19

March 20, 2020 / Leave a comment

Assignment 3

November 26, 2019 / Leave a comment

Nonstandard Normal Distributions

Here are nonstandard density curves with a mean equal to 15 and various standard deviations.
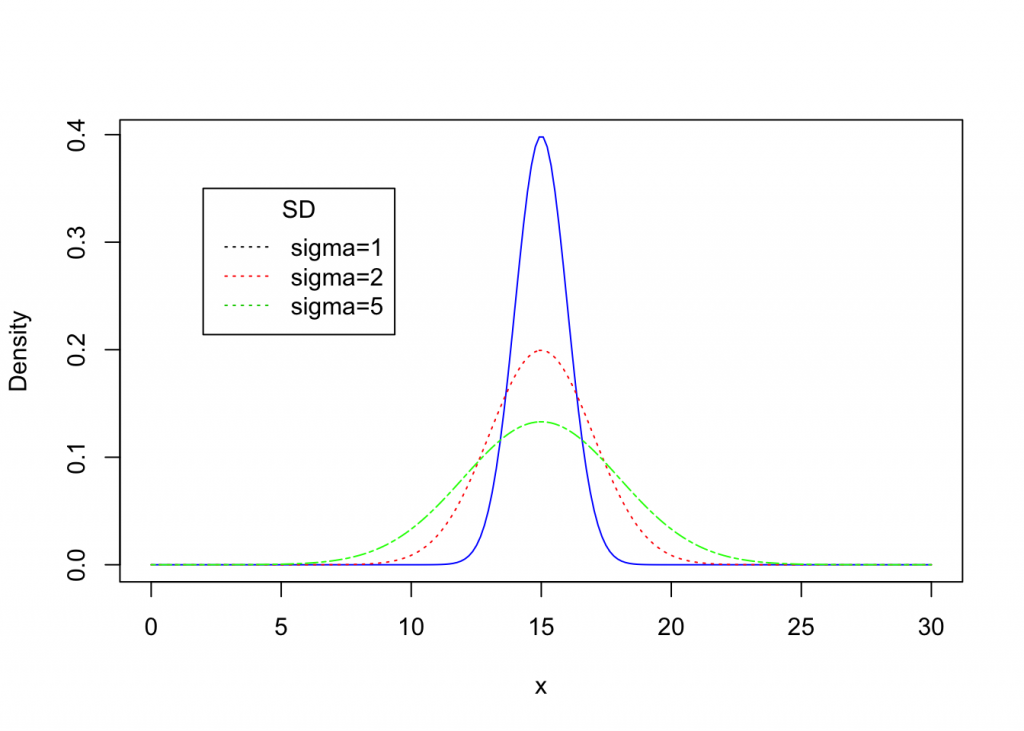
Model Problem1

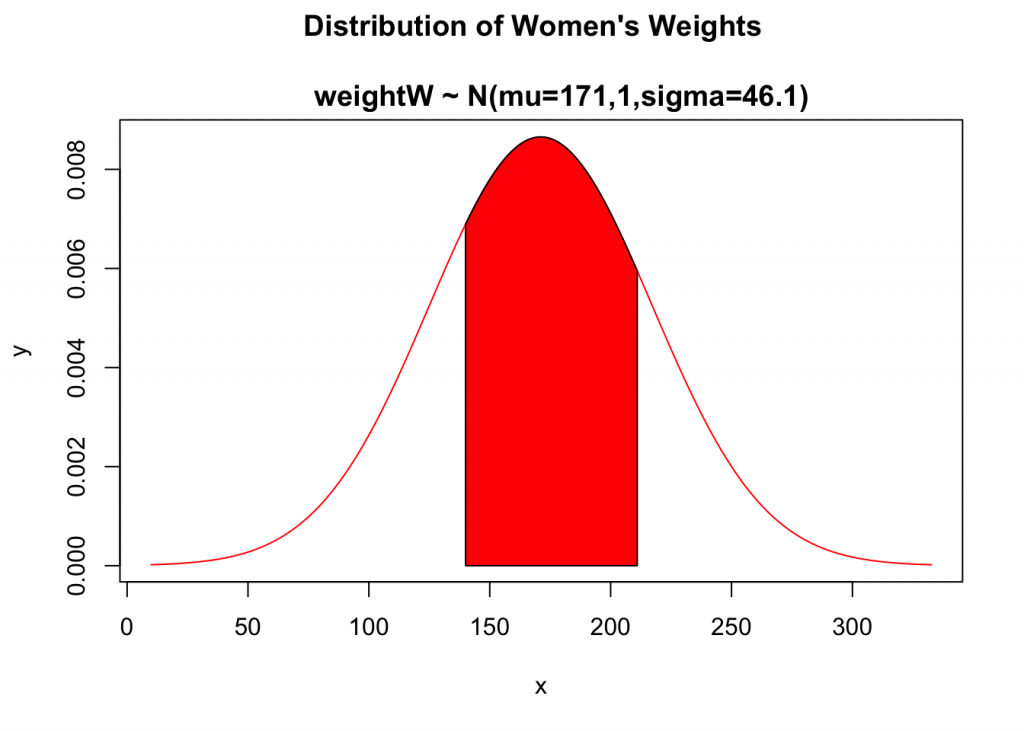
U.S. Air Force once used ACES-II ejection seats designed for men weighing between 140 lb and 211 lb. Given that women’s weights are normally distributed with a mean 171.1 lb and a standard deviation of 46.1 lb (based on data from the National Health Survey), what percentage of women have weights that are within those limits? Were many excluded from those past specifications?

Model Solution when Using z-tables

Given: Distribution Statement: heightW ~ N(mean = 171.1lb.,sd = 46.1lb.) and heightW boundaries: 140lb and 211lb

Objective(s): a. The proportion of women’s heights within the boundaries.
b. Were many women excluded from those past specifications?

Solution Plan

1. We will sketch and label nonstandard distribution of women’s heights, (heightW) and include distribution statement as its title.
2. Next, we will calculate z-scores for the boundaries and determine the area under density cure within these limits.

3. Finally, we will provide a written statement regarding obtained results.

1. Solution

Lower boundary: x=140
Upper boundary: x=211

2. Model solution when using z-tables

Now we will convert boundaries x=140 and x=211 to respective z-scores:

x = 140 corresponds to z = -0.67
x = 211 corresponds to z = 0.84

The area under the density curve within the limits is found from z-table it is equal to 0.5564. The cumulative area under both tails is 1 – 0.5564=0.4436

3. Statements about obtained results

3a. Just about 55.64% of women met past weight requirements.

3b. About 44.00% of women were excluded from past weight specifications.

Model Solution when Using R for Calculations

For part a. we will use: pnorm(x,mean,sd) code in the following way:

pnorm(211, mean=171.1, sd=46.1)-pnorm(140,mean=171.1, sd=46.1)
## [1] 0.556662

For part b we will use: code, 1- the previous answer:

1-0.556662
## [1] 0.443338

However, we may use more fancy code, (cut/paste) as follow:

1 -(pnorm(210, mean=171.1, sd=46.1)-pnorm(140,mean=171.1, sd=46.1))
## [1] 0.4493441

Assignment 3

Extra Credit: #29 and #33 from page: 252-253. Note: Follow model solution, part; (1), (2), and (3) in order to obtain full credit.

Extracted from M.F Triola, Essential s of Statistics Sixth Edition, Pearson. Essentials of Statistics page: 252, #27↩

  1. Extracted from M.F Triola, Essential s of Statistics Sixth Edition, Pearson. Essentials of Statistics page: 252, #27↩

Assignment 2

November 21, 2019 / 419 Comments on Assignment 2

The Normal Distribution

Here is the Standard Normal Distribution Density Curve is also known as the Bell Curve.

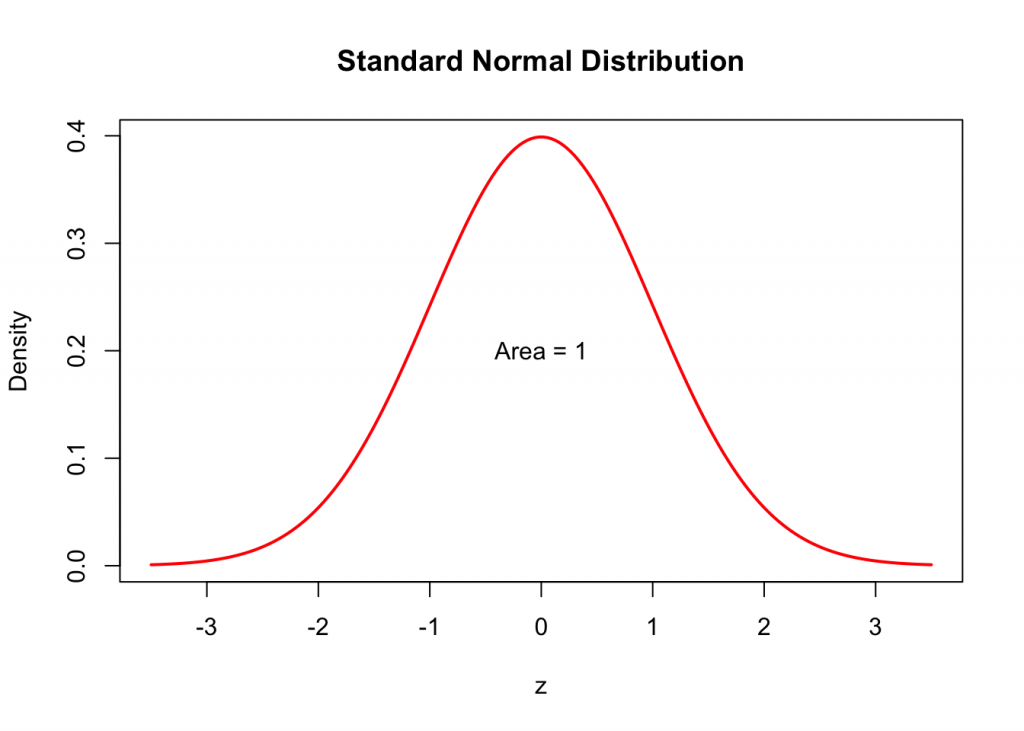
How do we find the area under the Standard Normal Density Curve?

Example 1
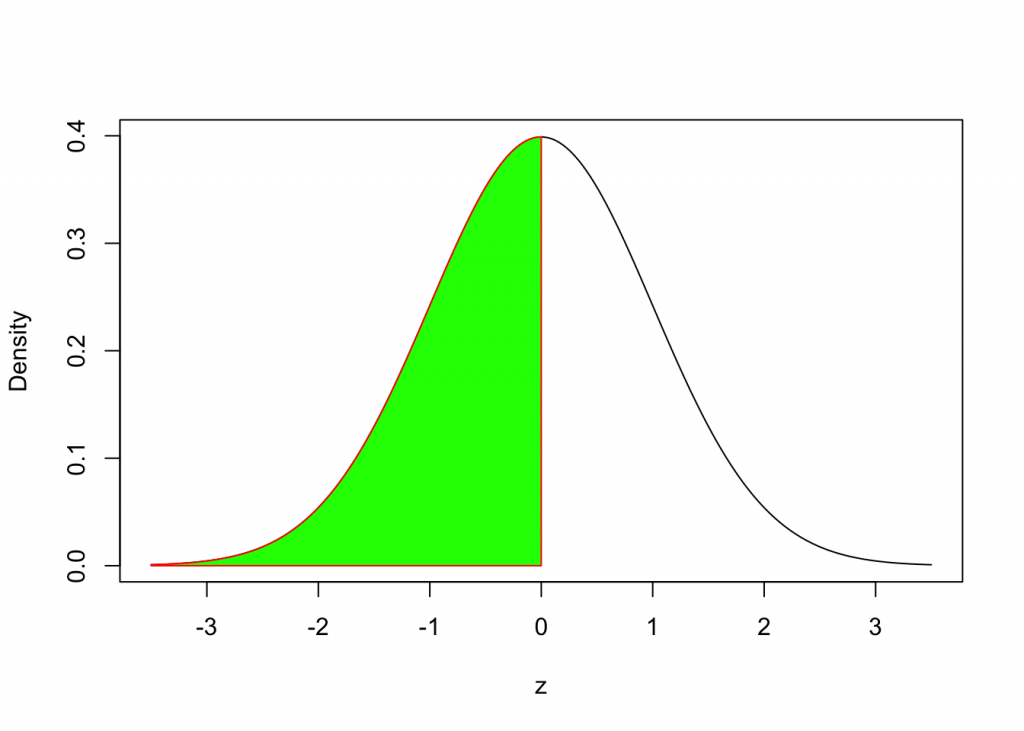
We will use the following syntax:
pnorm(0,mean=0,sd=1)
## [1] 0.5

Example 2

How do we find the area under the Standard Normal Density Curve to the left of z = 1.25?
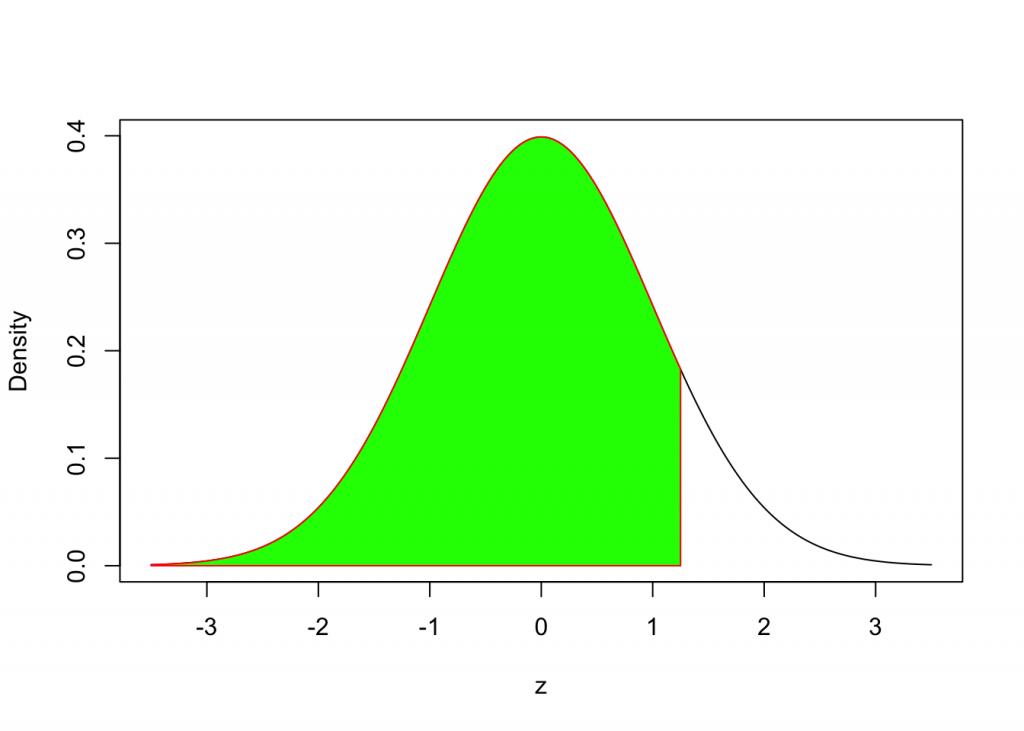
pnorm(1.25, mean=0,sd=1)
## [1] 0.8943502

Example 3

How do we find the area under the Standard Normal Density Curve to the right of z = 1.5?
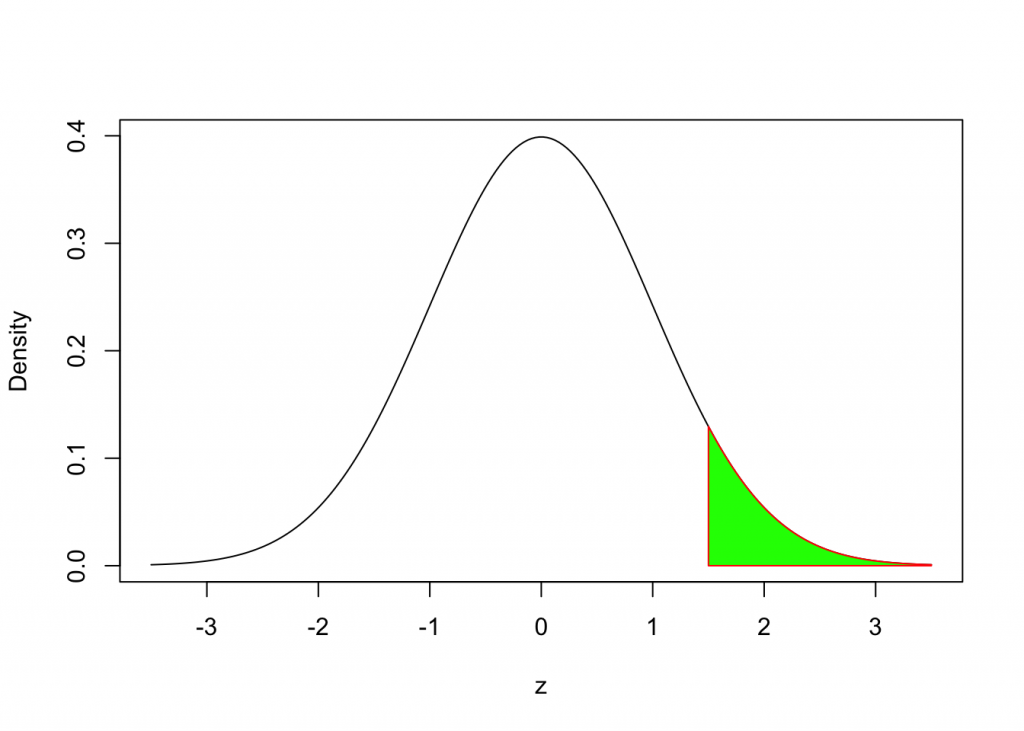
We can use the following syntax:
1 - pnorm(1.5, mean=0, sd=1)
## [1] 0.0668072
Alternatively the code below
pnorm(1.5, mean=0, sd = 1, lower.tail = FALSE)
## [1] 0.0668072

Example 4

How do we determine the area under the Standard Normal Curve between two z-values, (eg. z = -1.25 and z = 1.25)?
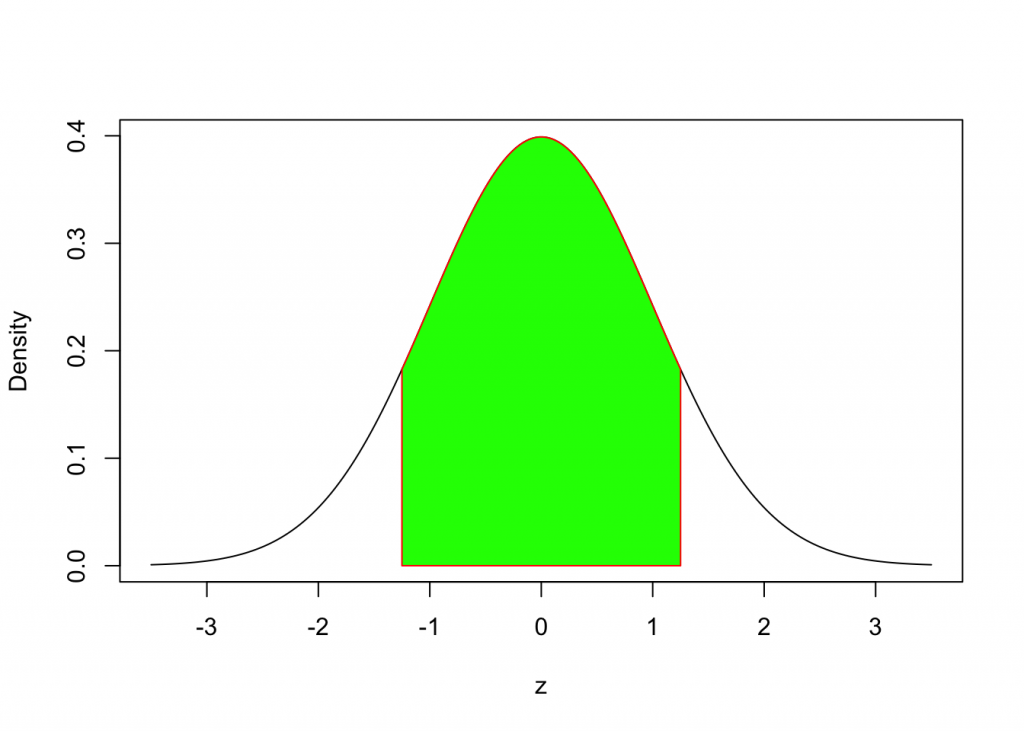
We can calculate the difference of two areas as follows:
pnorm(1.25, mean = 0, sd = 1) - pnorm(-1.25, mean = 0, sd = 1)
## [1] 0.7887005

Summary:

The following code pnorm(z, mean, sd) provides the area under the Standard Normal Density Curve to the left of z-value.

Assignment 2

The bone density test scores follow standard normal distribution for children, healthy premenopausal young women, and men under 50. Assume that a randomly selected person is subjected to a bone density test. Find the probability that this person has a score:

  1. z < -2.5
  2. -2.5 < z < -1
  3. z > -1.

Note: For each part: a, b and c include distribution statement, density curve with shaded area. Also, use a full and complete sentence as the answer to a, b, and c part.
link

Assignment 1

November 8, 2019 / Leave a comment

Tutorial/Extra Credit Assignment

How to partition Births Data Set1 by gender?

How to create a histogram of Birth Weight Data Set for each gender?

Upload data set by using the following syntax:

BirthsD <-read.csv(file.choose(),header =TRUE)

attach(BirthsD)
head(BirthsD,3)
##                         FACILITY         INSURANCE GENDER..1.M.
## 1 Albany Medical Center Hospital Insurance Company            0
## 2 Albany Medical Center Hospital        Blue Cross            1
## 3 Albany Medical Center Hospital        Blue Cross            0
##   LENGTH.OF.STAY ADMITTED DISCHARGED BIRTH.WEIGHT TOTAL.CHARGES
## 1              2      FRI        SUN         3500       13985.7
## 2              2      FRI        SUN         3900        3632.5
## 3             36      WED        THU          800      359091.0
Select all rows from the BirthsD data set that pertain to girls’ births and include all variables, (columns).
Start by naming this subset girlD, (girls data).
girlD <-BirthsD[GENDER..1.M. == "0",]
attach(girlD)
## The following objects are masked from BirthsD:
## 
##     ADMITTED, BIRTH.WEIGHT, DISCHARGED, FACILITY, GENDER..1.M.,
##     INSURANCE, LENGTH.OF.STAY, TOTAL.CHARGES
head(girlD)
##                          FACILITY         INSURANCE GENDER..1.M.
## 1  Albany Medical Center Hospital Insurance Company            0
## 3  Albany Medical Center Hospital        Blue Cross            0
## 6  Albany Medical Center Hospital        Blue Cross            0
## 7  Albany Medical Center Hospital          Medicaid            0
## 9  Albany Medical Center Hospital Insurance Company            0
## 13 Albany Medical Center Hospital Insurance Company            0
##    LENGTH.OF.STAY ADMITTED DISCHARGED BIRTH.WEIGHT TOTAL.CHARGES
## 1               2      FRI        SUN         3500       13985.7
## 3              36      WED        THU          800      359091.0
## 6               4      FRI        TUE         2400        6406.0
## 7               3      TUE        FRI         4200        4778.0
## 9               2      SAT        MON         3100        3860.0
## 13              4      SUN        THU         2000        6986.9
summary(BIRTH.WEIGHT)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##     300    2700    3100    3037    3500    4700
Create a frequency table for Girls’ birth weights.
breaks <-seq(0,5000,by=500)
BIRTH.WEIGHT.cut <-cut(BIRTH.WEIGHT,breaks)
BIRTH.WEIGHT.freq <-table(BIRTH.WEIGHT.cut)
frequency.table <-transform(BIRTH.WEIGHT.freq)
frequency.table
##    BIRTH.WEIGHT.cut Freq
## 1           (0,500]    1
## 2       (500,1e+03]    5
## 3   (1e+03,1.5e+03]    1
## 4   (1.5e+03,2e+03]   12
## 5   (2e+03,2.5e+03]   19
## 6   (2.5e+03,3e+03]   50
## 7   (3e+03,3.5e+03]   75
## 8   (3.5e+03,4e+03]   33
## 9   (4e+03,4.5e+03]    7
## 10  (4.5e+03,5e+03]    2
Create a histogram of birth weights for girls’ data subset using breaks and hist command.
breaks<-seq(0,5000,by=500)
hist(BIRTH.WEIGHT, xlab = "Birth Weight in [grams]", ylab="Frequency",ylim=c(0,80),main="Distribution of Birth Weights for Girls", col="pink",border="blue")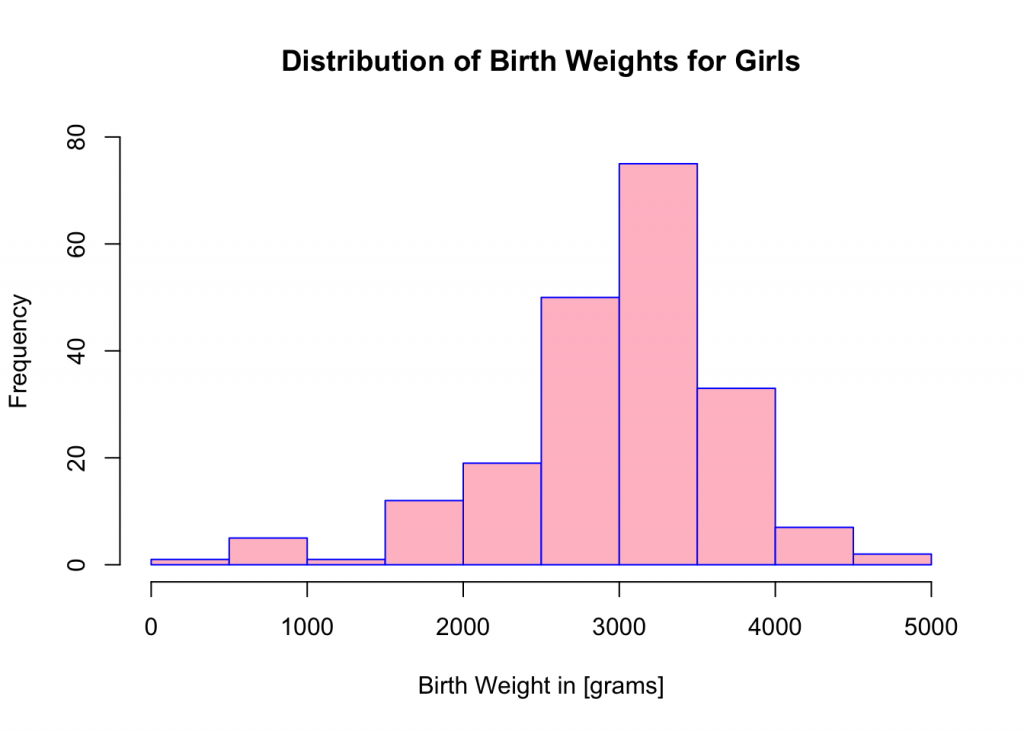
detach(girlD)
Now: Select all rows from BirthsD data set that pertain to boys’ births and include all variables, (columns).

Start by naming this subset boyD, (boys’ data).

boyD <-BirthsD[GENDER..1.M. == "1", ]
attach(boyD)
## The following objects are masked from BirthsD:
## 
##     ADMITTED, BIRTH.WEIGHT, DISCHARGED, FACILITY, GENDER..1.M.,
##     INSURANCE, LENGTH.OF.STAY, TOTAL.CHARGES
head(boyD,3)
##                         FACILITY         INSURANCE GENDER..1.M.
## 2 Albany Medical Center Hospital        Blue Cross            1
## 4 Albany Medical Center Hospital Insurance Company            1
## 5 Albany Medical Center Hospital Insurance Company            1
##   LENGTH.OF.STAY ADMITTED DISCHARGED BIRTH.WEIGHT TOTAL.CHARGES
## 2              2      FRI        SUN         3900        3632.5
## 4              5      MON        SAT         2800        8536.5
## 5              2      FRI        SUN         3700        3632.5
summary(BIRTH.WEIGHT)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##     300    2900    3400    3273    3650    4900
Create a frequency table for Boys’ birth weights.
BIRTH.WEIGHT.cut <-cut(BIRTH.WEIGHT,breaks)
BIRTH.WEIGHT.freq <-table(BIRTH.WEIGHT.cut)
transform(BIRTH.WEIGHT.freq)
##    BIRTH.WEIGHT.cut Freq
## 1           (0,500]    1
## 2       (500,1e+03]    2
## 3   (1e+03,1.5e+03]    2
## 4   (1.5e+03,2e+03]    5
## 5   (2e+03,2.5e+03]    8
## 6   (2.5e+03,3e+03]   39
## 7   (3e+03,3.5e+03]   69
## 8   (3.5e+03,4e+03]   57
## 9   (4e+03,4.5e+03]   10
## 10  (4.5e+03,5e+03]    2
Create a histogram of birth weights for boys data subset using breaks and hist command.
breaks<-seq(0,5000,by=500)
hist(BIRTH.WEIGHT, xlab = "Birth Weight in [grams]", ylab="Frequency",ylim=c(0,80),main="Distribution of Birth Weights for Boys", col="blue",border="yellow")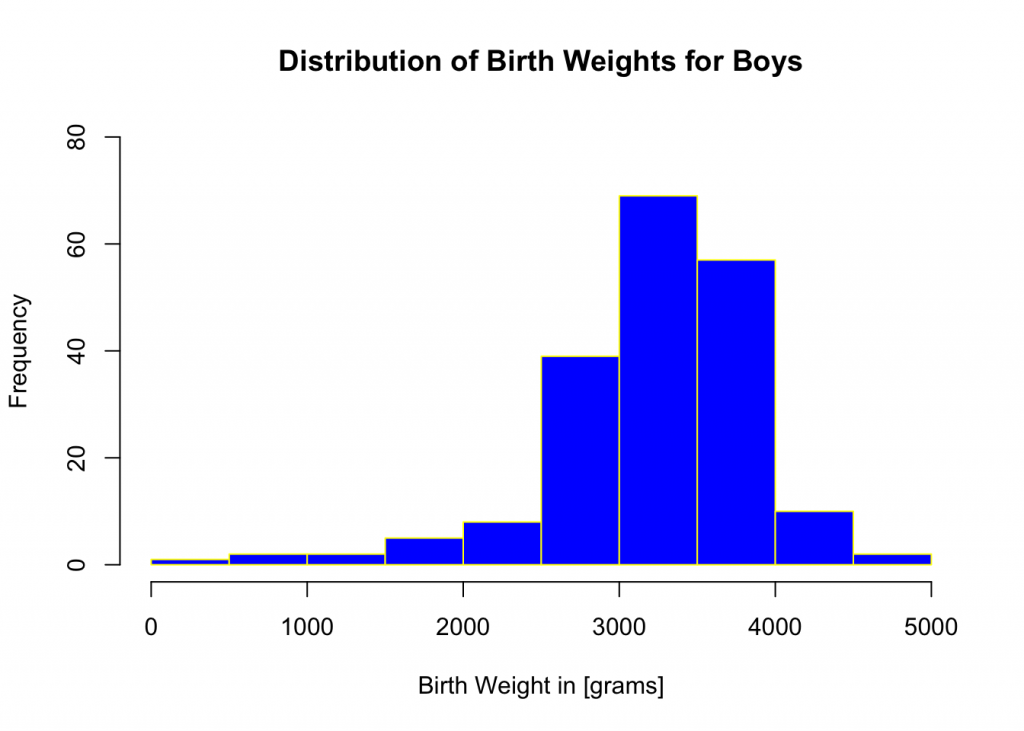
detach(boyD)

Extra Credit Assignment

1. Use parts of the above syntax and create two box-and-whisker plots, (one for each gender), describe variability in each subset, and compare variability between genders.
2. Write a report using any word-processing program. Use full and complete sentences; remember to include numerical and graphical summaries in your report. In addition, attach R printout with input/output.
  1. Data Set 4: extracted from M. F Triola, Essentials of Statistics Sixth Edition, Pearson↩