Frequency Table Using R Part2
How Do We Construct Frequency Distribution Tables Using R?
Part 2 (Relative Frequeancy Distribution Table, Cumulative Frequency Distribution, and Cumulative Relative Frequency Distribution Table)
We will use States Visited, (StatesV) variable included in first day class survey, Sur1.
- Upload Sur1.csv data set from your desktop to R
Sur1 <-read.csv("~/Desktop/Sur1.csv")NOTE: If case you did not save Sur1.csv file correctly to your desktop, execute the following code
Sur1 <-read.csv(read.csv(file.choose(),header = TRUE))
- Examinne the strucure of Sur1 data set
str(Sur1)## 'data.frame': 20 obs. of 6 variables:
## $ SEX : Factor w/ 2 levels "Female","Male": 1 1 1 1 2 2 2 1 1 1 ...
## $ POLITICS : Factor w/ 3 levels "Conservative",..: 3 3 3 3 3 3 2 2 1 3 ...
## $ NSiblings: int 4 4 2 2 2 4 5 4 4 1 ...
## $ StatesV : int 5 11 6 3 7 3 4 4 6 3 ...
## $ ShoeS : num 6 9 8 7.5 13 10.5 9 8 6 8.5 ...
## $ UsedExcel: int 2 2 2 1 1 3 3 2 2 1 ...- View first six row of the data in spreadsheet format
head(Sur1, 6)## SEX POLITICS NSiblings StatesV ShoeS UsedExcel
## 1 Female Moderate 4 5 6.0 2
## 2 Female Moderate 4 11 9.0 2
## 3 Female Moderate 2 6 8.0 2
## 4 Female Moderate 2 3 7.5 1
## 5 Male Moderate 2 7 13.0 1
## 6 Male Moderate 4 3 10.5 3- Attach Sur1 to R in order to work with data variables without using $ symbol (remember to detach(Sur1) after completion of analysis)
attach(Sur1)- Summarize StatesV variable
summary(StatesV)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 3.00 4.00 6.00 7.15 9.50 18.00- Construct a frequency distribution table of States Visited using breaks to list class limits
breaks <-seq(0,18, by=3)- Group StatesV variable data into bins
StatesV.cut <-cut(StatesV,breaks)- Construct frequency table for StatesV variable in horizontal display
table(StatesV.cut)## StatesV.cut
## (0,3] (3,6] (6,9] (9,12] (12,15] (15,18]
## 3 8 4 3 1 1- Transform this table to 2-column display
transform(table(StatesV.cut))## StatesV.cut Freq
## 1 (0,3] 3
## 2 (3,6] 8
## 3 (6,9] 4
## 4 (9,12] 3
## 5 (12,15] 1
## 6 (15,18] 1- Convert frequency table to relative frequency table by dividing frequencies by total number of StatesV data, in our case by 20
transform(table(StatesV.cut)/20)## StatesV.cut Freq
## 1 (0,3] 0.15
## 2 (3,6] 0.40
## 3 (6,9] 0.20
## 4 (9,12] 0.15
## 5 (12,15] 0.05
## 6 (15,18] 0.05- Convert frequency table to cumulative frequency table by summing frequencies of StatesV data cumulatively
transform(table(StatesV.cut),Cum_Freq=cumsum(Freq))## StatesV.cut Freq Cum_Freq
## 1 (0,3] 3 3
## 2 (3,6] 8 11
## 3 (6,9] 4 15
## 4 (9,12] 3 18
## 5 (12,15] 1 19
## 6 (15,18] 1 20- Convert frequency table to cumulative relative frequency table by dividing cumulative frequencies by total number of StatesV data, in our case by 20
transform(table(StatesV.cut),RelCum_Freq=cumsum(Freq)/20)## StatesV.cut Freq RelCum_Freq
## 1 (0,3] 3 0.15
## 2 (3,6] 8 0.55
## 3 (6,9] 4 0.75
## 4 (9,12] 3 0.90
## 5 (12,15] 1 0.95
## 6 (15,18] 1 1.00Frequency Tables Using R Part 1
How Do We Construct A Frequency Distribution Table Using R? Part 1
We will use States Visited, (StatesV) variables included in the first-day class survey, Sur1.
- Upload Sur1.csv data set from your desktop to R
Sur1 <-read.csv("~/Desktop/Sur1.csv")NOTE: In case you did not save Sur1.csv file correctly to your desktop, execute the following code
Sur1 <-read.csv(read.csv(file.choose(),header = TRUE))
- Examinne the strucure of Sur1 data set
str(Sur1)## 'data.frame': 20 obs. of 6 variables:
## $ SEX : Factor w/ 2 levels "Female","Male": 1 1 1 1 2 2 2 1 1 1 ...
## $ POLITICS : Factor w/ 3 levels "Conservative",..: 3 3 3 3 3 3 2 2 1 3 ...
## $ NSiblings: int 4 4 2 2 2 4 5 4 4 1 ...
## $ StatesV : int 5 11 6 3 7 3 4 4 6 3 ...
## $ ShoeS : num 6 9 8 7.5 13 10.5 9 8 6 8.5 ...
## $ UsedExcel: int 2 2 2 1 1 3 3 2 2 1 ...- View first six row of the data in spreadsheet format
head(Sur1, 6)## SEX POLITICS NSiblings StatesV ShoeS UsedExcel
## 1 Female Moderate 4 5 6.0 2
## 2 Female Moderate 4 11 9.0 2
## 3 Female Moderate 2 6 8.0 2
## 4 Female Moderate 2 3 7.5 1
## 5 Male Moderate 2 7 13.0 1
## 6 Male Moderate 4 3 10.5 3- Attach Sur1 to R in order to work with data variables without using $ symbol (remember to detach(Sur1) after completion of analysis)
attach(Sur1)- Summarize StatesV variable
summary(StatesV)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 3.00 4.00 6.00 7.15 9.50 18.00- Construct a frequency distribution table of States Visited using breaks to list class limits
breaks <-seq(0,18, by=3)- Group StatesV variable data into bins
StatesV.cut <-cut(StatesV,breaks)- Construct frequency table for StatesV variable in horizontal display
table(StatesV.cut)## StatesV.cut
## (0,3] (3,6] (6,9] (9,12] (12,15] (15,18]
## 3 8 4 3 1 1- Transform this table to 2-column display
transform(table(StatesV.cut))## StatesV.cut Freq
## 1 (0,3] 3
## 2 (3,6] 8
## 3 (6,9] 4
## 4 (9,12] 3
## 5 (12,15] 1
## 6 (15,18] 1- Construct a histogram of the frequency distribution of StatesV variable
hist(StatesV,breaks,col="red",border = "blue",xlab="Number of States Visited",xlim = c(0,21),ylab="Frequency",main="Distribution of States Visited by Mat150-1701 Students")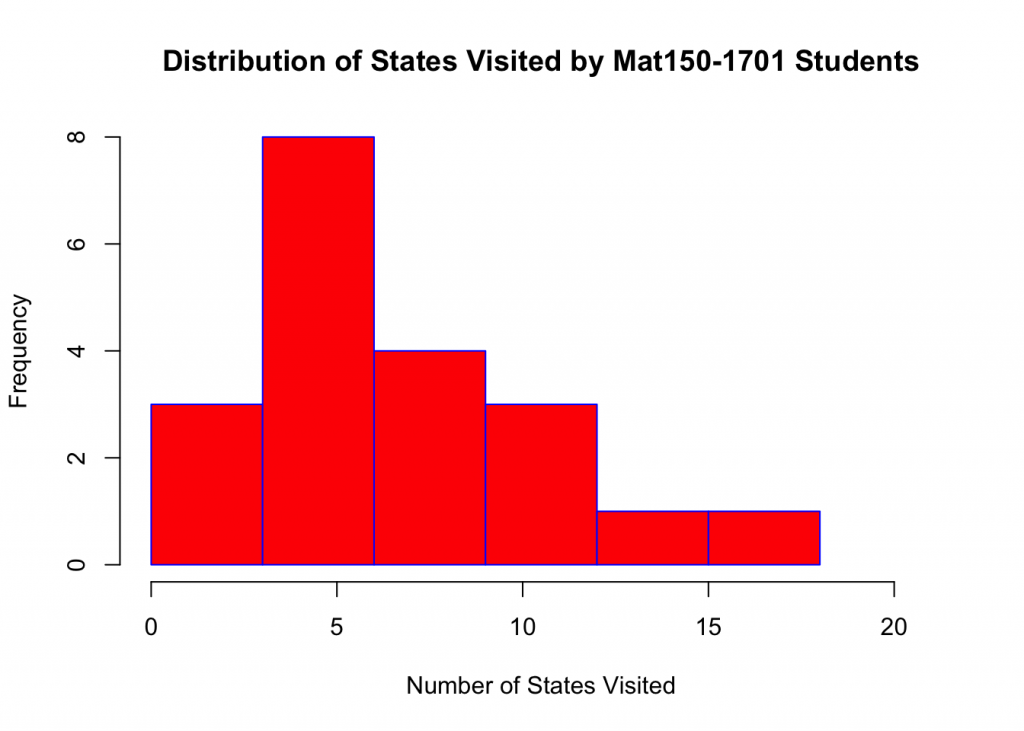
Uploading a .csv file into R
Day 1: Using R as Calculator (We will not save files in R format for now!)
Objective: How to upload a .csv file into R?
Step 1 Prepare your workspace
Whenever you begin/complete your work with R execute these two commands: rm(list=ls()) and ls() .
Launch R and type into console panel:
rm(list=ls())
press ENTER key, then check if your workspace is cleared
by using:
ls()
Step 2 Upload survey data, Sur1.csv by using following syntax
Sur1 <-read.csv(file.choose(),header=TRUE)
Note: You must have your .csv file already downloaded to your computer, (e.g. to your desktop).
Step 3 Check the structure of data uploaded by using the following code
Str(Sur1)
Step 4 Optional: Verify names of variables included in data by using the following syntax
names(Sur1)
Step 5 View the first five rows of Sur1 data using the following syntax:
head(Sur1, 5)
Step 6
Attach Sur1 data in order to use names of respected variables without $ sign
attach(Sur1)
Step 7 Get a quick look at the summary of variables of Sur1
- summary(Sur1)
Tutorial 2
Sampling Distribution of Sample Mean
Example 1 (Data Set 21)
- Upload Data Set 21 to R in previously saved .csv format.
- Use Data Set 21 to construct a histogram of DEPTHS of 600 earthquakes.
- Select 10000 random samples of size=50 from the DEPTHS variable, calculate the mean of each and construct a histogram of the sampling distribution of the sample means.
SOLUTION
EarthQ <- read.csv("~/Desktop/csv/21 - Earthquakes.csv")attach(EarthQ)head(EarthQ)## MAGNITUDE DEPTH
## 1 2.45 0.7
## 2 3.62 6.0
## 3 3.06 7.0
## 4 3.30 5.4
## 5 1.09 0.5
## 6 3.10 0.02. breaks <-seq(0,45,by=5)
hist(DEPTH,breaks, col="red",xlab = "Depth [km]",ylab = "Frequency",main = "Histogram of Earthquakes Depths")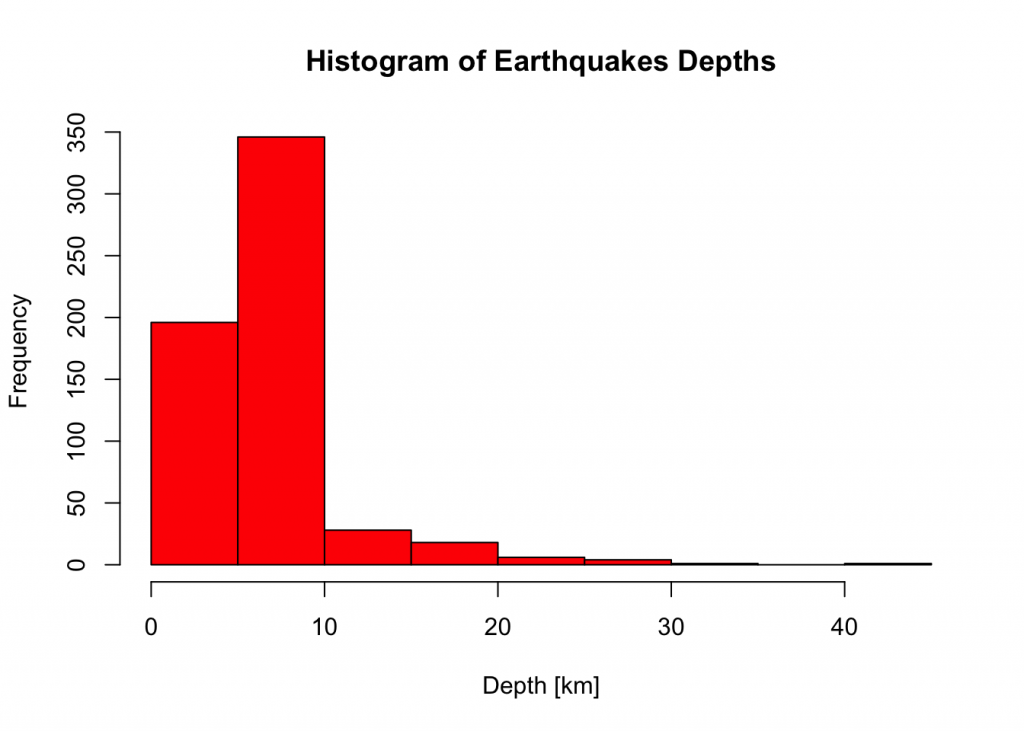
mean(DEPTH)## [1] 5.822sd(DEPTH)## [1] 4.927049fifty.depths <- function() {
depth.S <- sample(DEPTH,
size = 50,replace = TRUE)
return(mean(depth.S))
} sim1 <-replicate(n=10000,expr=fifty.depths())head(sim1)## [1] 5.540 6.576 5.224 6.800 5.262 4.952summary(sim1)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 3.650 5.338 5.798 5.825 6.270 8.742sd(sim1)## [1] 0.695623breaks <-seq(2.5,10.5,by=0.5)
hist(sim1,breaks,xlab ="Mean[km]",ylab="Frequency",col="red",border = "green",main="Sampling Distribution of the Sample Mean")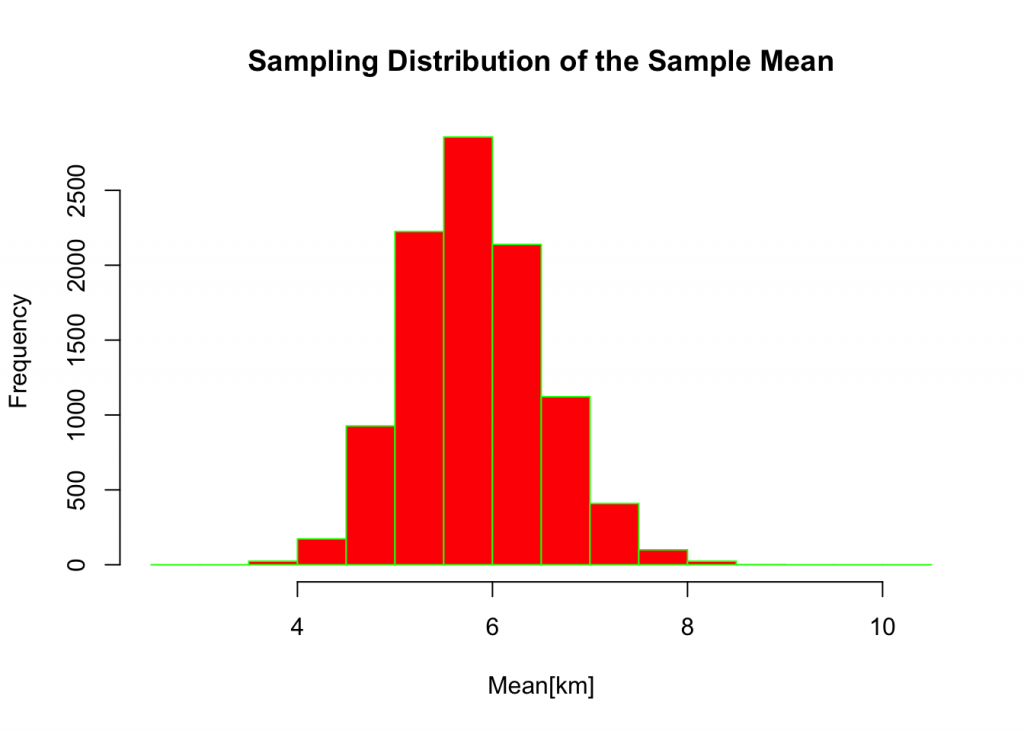
Things to ponder:
- the shape of DEPTH histogram
- values of the mean(DEPTH) and sd(DEPTH)
- shape of means(DEPTH) sampling distribution
- values of the mean of the sampling distribution and standard deviation of the sampling distribution
Tutorial 1
Five fair dice were rolled once and the proportion of ODD outcomes was observed.
Example 1
x <-sample(1:6,5,replace = TRUE); x## [1] 5 2 2 5 4What is the proportion of ODD outcomes?
y <- x %% 2;y## [1] 1 0 0 1 0prop <-sum(y)/length(x);prop## [1] 0.4Example 2 (Simulation)
Replicate 100,000 five-dice rolls and record the proportion of ODD numbers for each roll.
five.dice <- function() {
dice <-sample(1:6,5, replace = TRUE)
return(sum(dice %% 2)/length(dice))
}
sim1 <-replicate(100000, five.dice())Here are the first six recorded proportions of ODD outcomes.
head(sim1)## [1] 0.2 0.6 0.4 0.6 0.2 1.0Table of Proportions of ODD outcomes from 100,000 simulated rolls
transform(table(sim1))## sim1 Freq
## 1 0 3065
## 2 0.2 15541
## 3 0.4 31303
## 4 0.6 31434
## 5 0.8 15626
## 6 1 3031Histogram of Proportions of ODD Outcomes
breaks <-seq(-0.1,1.1,by=0.2)
hist(sim1,breaks, col="red", border = "green",xlab="Proportion of ODD Numbers",ylab="Frequency", main = "Sampling Distribution of Sample Proportion")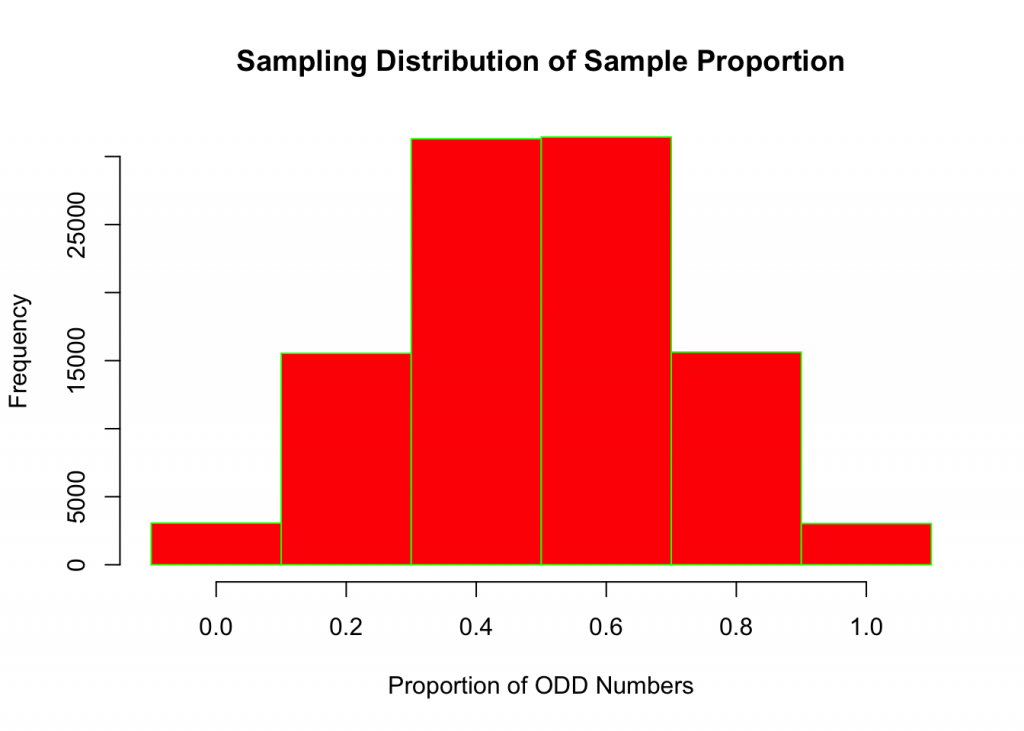
Finally, the mean proportion of simulated proportions is equal to:
mean(sim1)## [1] 0.500216Ponder on the following: a) shape of the sampling distribution of the sample proportion
b) the mean proportion of the sample proportion
c) proportion of ODD outcomes when rolling a fair die once
d) writing a simulation like the one above regarding the proportion of EVEN outcomes in 100,000 rolls of five-fair dice.
Assignment 3
Nonstandard Normal Distributions
Here are nonstandard density curves with a mean equal to 15 and various standard deviations.
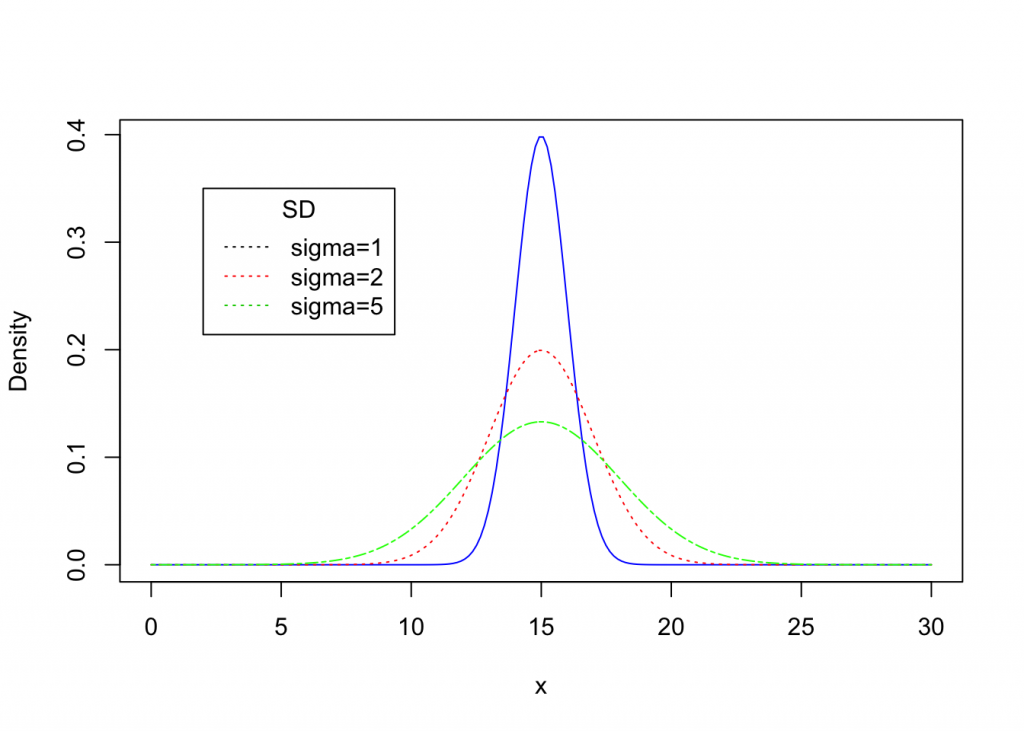
Model Problem1
U.S. Air Force once used ACES-II ejection seats designed for men weighing between 140 lb and 211 lb. Given that women’s weights are normally distributed with a mean 171.1 lb and a standard deviation of 46.1 lb (based on data from the National Health Survey), what percentage of women have weights that are within those limits? Were many excluded from those past specifications?
Model Solution when Using z-tables
Given: Distribution Statement: heightW ~ N(mean = 171.1lb.,sd = 46.1lb.) and heightW boundaries: 140lb and 211lb
Objective(s): a. The proportion of women’s heights within the boundaries.
b. Were many women excluded from those past specifications?
Solution Plan
1. We will sketch and label nonstandard distribution of women’s heights, (heightW) and include distribution statement as its title.
2. Next, we will calculate z-scores for the boundaries and determine the area under density cure within these limits.
3. Finally, we will provide a written statement regarding obtained results.
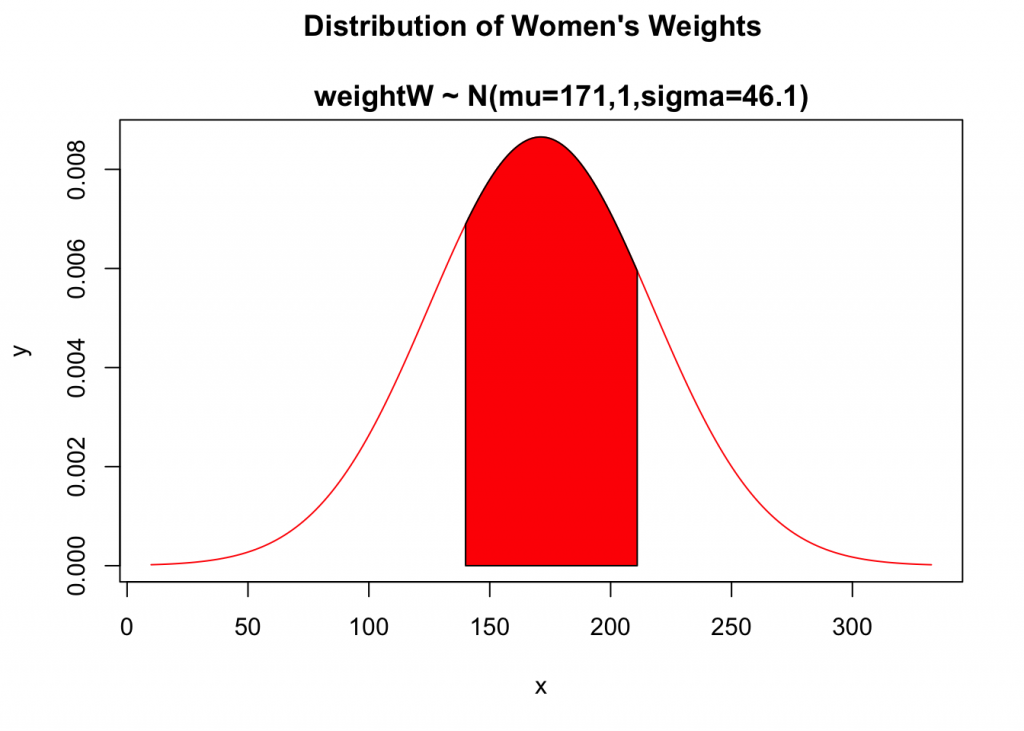
1. Solution
Lower boundary: x=140
Upper boundary: x=211
2. Model solution when using z-tables
Now we will convert boundaries x=140 and x=211 to respective z-scores:
x = 140 corresponds to z = -0.67
x = 211 corresponds to z = 0.84
The area under the density curve within the limits is found from z-table it is equal to 0.5564. The cumulative area under both tails is 1 – 0.5564=0.4436
3. Statements about obtained results
3a. Just about 55.64% of women met past weight requirements.
3b. About 44.00% of women were excluded from past weight specifications.
Model Solution when Using R for Calculations
For part a. we will use: pnorm(x,mean,sd) code in the following way:
pnorm(211, mean=171.1, sd=46.1)-pnorm(140,mean=171.1, sd=46.1)## [1] 0.556662For part b we will use: code, 1- the previous answer:
1-0.556662## [1] 0.443338However, we may use more fancy code, (cut/paste) as follow:
1 -(pnorm(210, mean=171.1, sd=46.1)-pnorm(140,mean=171.1, sd=46.1))## [1] 0.4493441Assignment 3
Extra Credit: #29 and #33 from page: 252-253. Note: Follow model solution, part; (1), (2), and (3) in order to obtain full credit.
Extracted from M.F Triola, Essential s of Statistics Sixth Edition, Pearson. Essentials of Statistics page: 252, #27↩
- Extracted from M.F Triola, Essential s of Statistics Sixth Edition, Pearson. Essentials of Statistics page: 252, #27↩
Assignment 2
The Normal Distribution
Here is the Standard Normal Distribution Density Curve is also known as the Bell Curve.
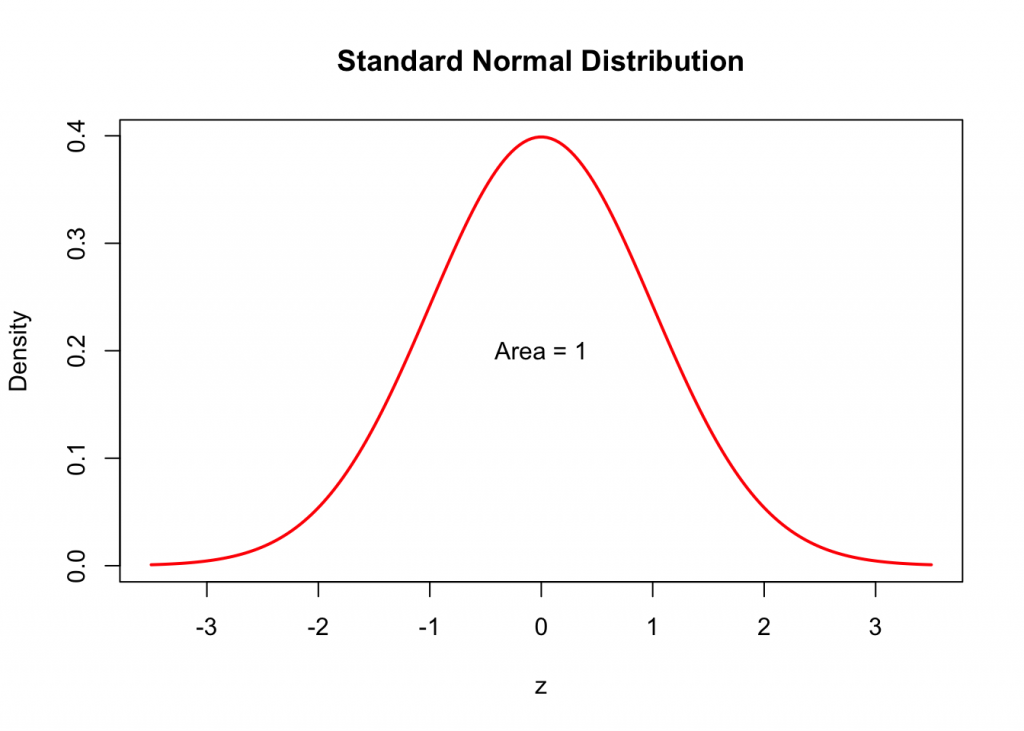
How do we find the area under the Standard Normal Density Curve?
Example 1
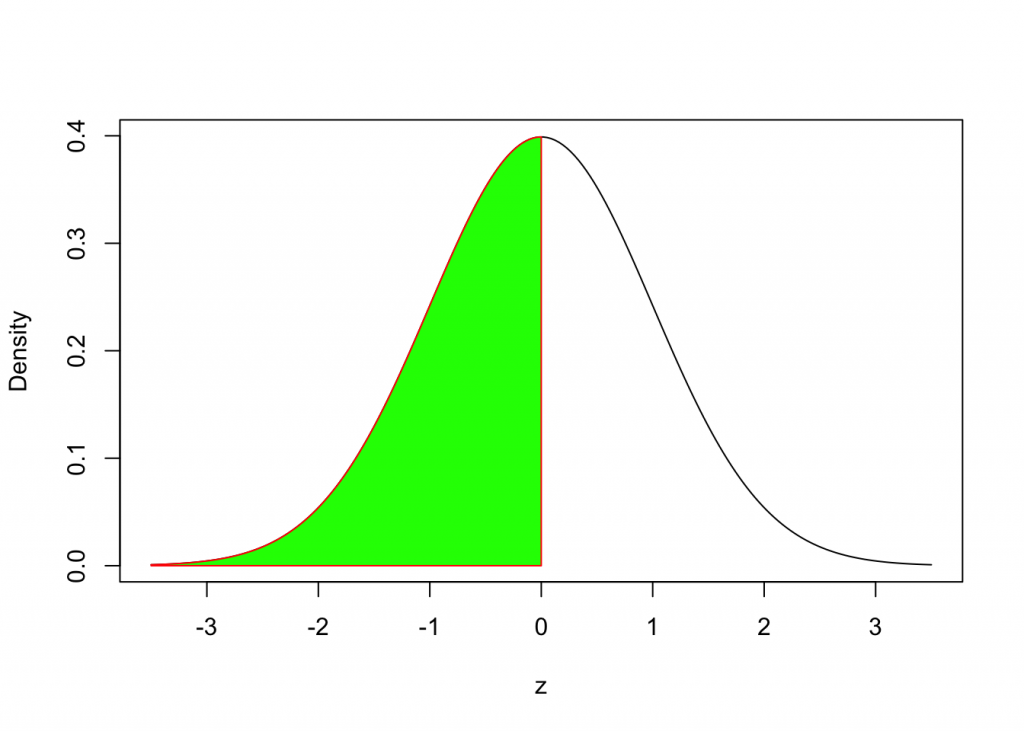
We will use the following syntax:
pnorm(0,mean=0,sd=1)## [1] 0.5Example 2
How do we find the area under the Standard Normal Density Curve to the left of z = 1.25?
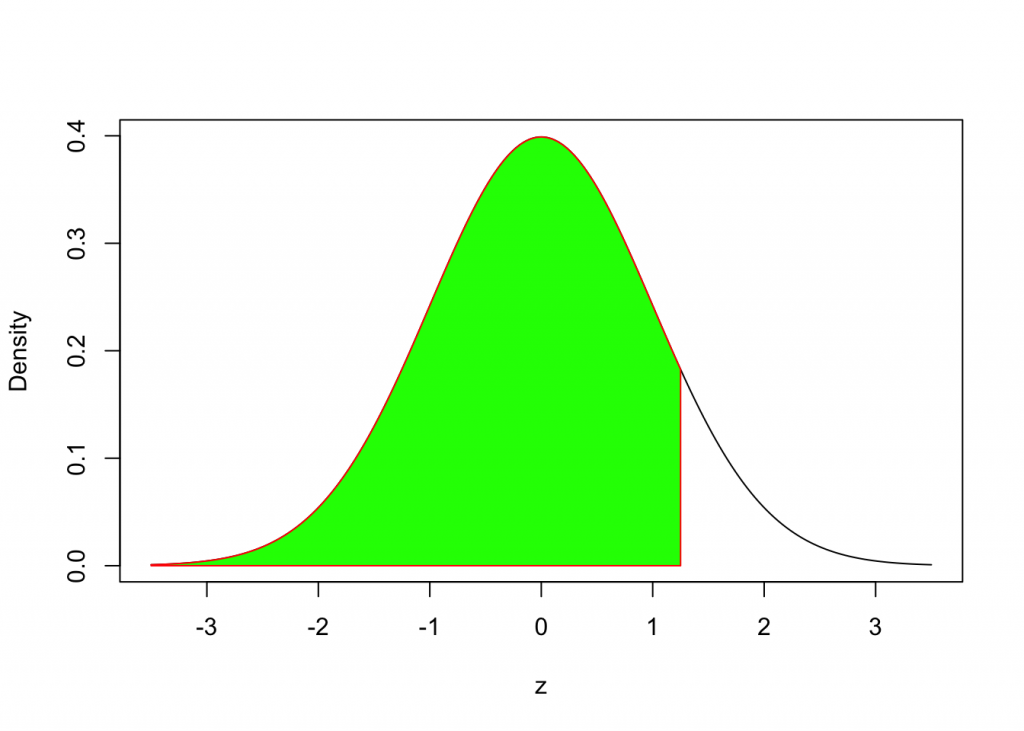
pnorm(1.25, mean=0,sd=1)## [1] 0.8943502Example 3
How do we find the area under the Standard Normal Density Curve to the right of z = 1.5?
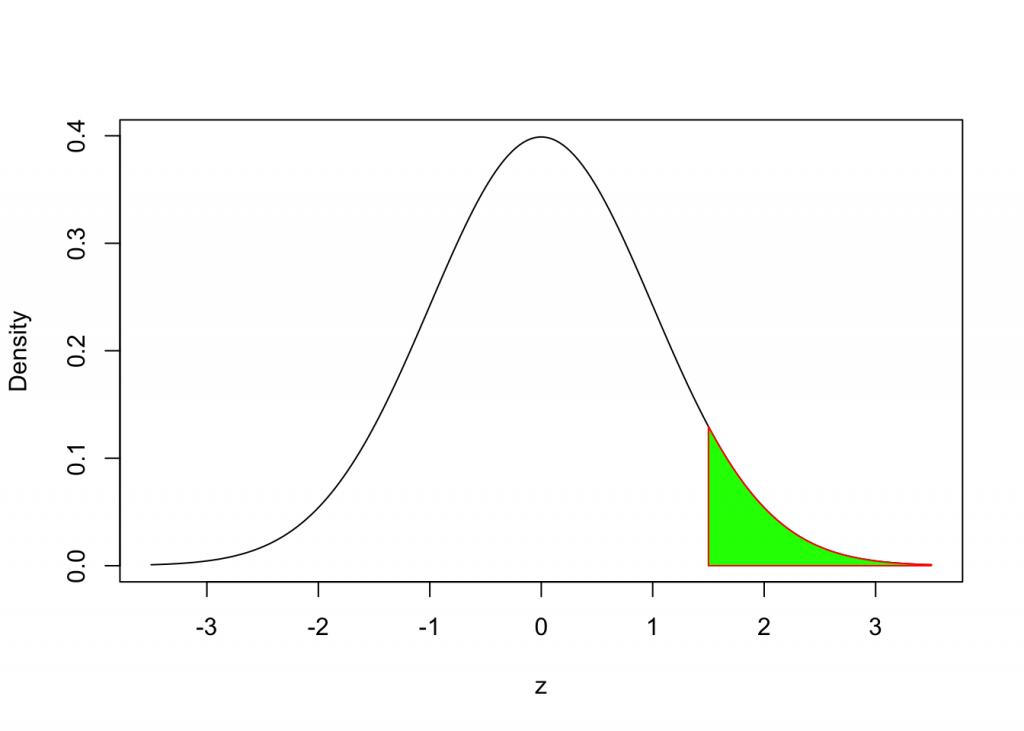
We can use the following syntax:
1 - pnorm(1.5, mean=0, sd=1)## [1] 0.0668072Alternatively the code below
pnorm(1.5, mean=0, sd = 1, lower.tail = FALSE)## [1] 0.0668072Example 4
How do we determine the area under the Standard Normal Curve between two z-values, (eg. z = -1.25 and z = 1.25)?
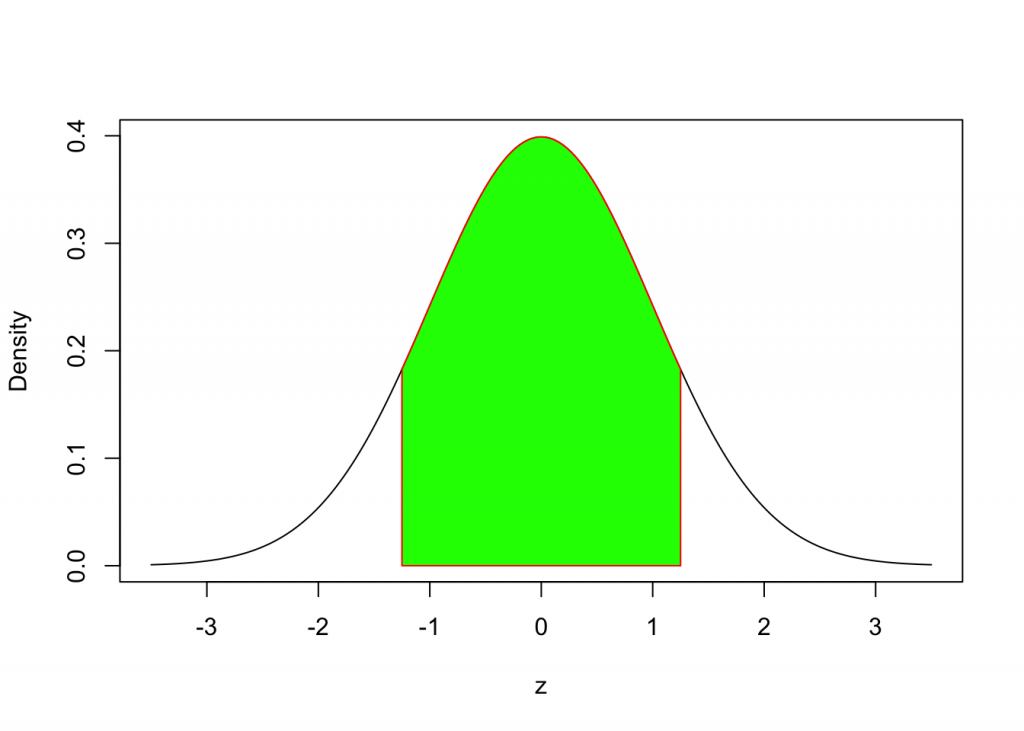
We can calculate the difference of two areas as follows:
pnorm(1.25, mean = 0, sd = 1) - pnorm(-1.25, mean = 0, sd = 1)## [1] 0.7887005Summary:
The following code pnorm(z, mean, sd) provides the area under the Standard Normal Density Curve to the left of z-value.
Assignment 2
The bone density test scores follow standard normal distribution for children, healthy premenopausal young women, and men under 50. Assume that a randomly selected person is subjected to a bone density test. Find the probability that this person has a score:
- z < -2.5
- -2.5 < z < -1
- z > -1.
Note: For each part: a, b and c include distribution statement, density curve with shaded area. Also, use a full and complete sentence as the answer to a, b, and c part.
link
Assignment 1
Tutorial/Extra Credit Assignment
How to partition Births Data Set1 by gender?
How to create a histogram of Birth Weight Data Set for each gender?
Upload data set by using the following syntax:
BirthsD <-read.csv(file.choose(),header =TRUE)
attach(BirthsD)
head(BirthsD,3)## FACILITY INSURANCE GENDER..1.M.
## 1 Albany Medical Center Hospital Insurance Company 0
## 2 Albany Medical Center Hospital Blue Cross 1
## 3 Albany Medical Center Hospital Blue Cross 0
## LENGTH.OF.STAY ADMITTED DISCHARGED BIRTH.WEIGHT TOTAL.CHARGES
## 1 2 FRI SUN 3500 13985.7
## 2 2 FRI SUN 3900 3632.5
## 3 36 WED THU 800 359091.0Select all rows from the BirthsD data set that pertain to girls’ births and include all variables, (columns).
Start by naming this subset girlD, (girls data).
girlD <-BirthsD[GENDER..1.M. == "0",]
attach(girlD)## The following objects are masked from BirthsD:
##
## ADMITTED, BIRTH.WEIGHT, DISCHARGED, FACILITY, GENDER..1.M.,
## INSURANCE, LENGTH.OF.STAY, TOTAL.CHARGEShead(girlD)## FACILITY INSURANCE GENDER..1.M.
## 1 Albany Medical Center Hospital Insurance Company 0
## 3 Albany Medical Center Hospital Blue Cross 0
## 6 Albany Medical Center Hospital Blue Cross 0
## 7 Albany Medical Center Hospital Medicaid 0
## 9 Albany Medical Center Hospital Insurance Company 0
## 13 Albany Medical Center Hospital Insurance Company 0
## LENGTH.OF.STAY ADMITTED DISCHARGED BIRTH.WEIGHT TOTAL.CHARGES
## 1 2 FRI SUN 3500 13985.7
## 3 36 WED THU 800 359091.0
## 6 4 FRI TUE 2400 6406.0
## 7 3 TUE FRI 4200 4778.0
## 9 2 SAT MON 3100 3860.0
## 13 4 SUN THU 2000 6986.9summary(BIRTH.WEIGHT)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 300 2700 3100 3037 3500 4700Create a frequency table for Girls’ birth weights.
breaks <-seq(0,5000,by=500)
BIRTH.WEIGHT.cut <-cut(BIRTH.WEIGHT,breaks)
BIRTH.WEIGHT.freq <-table(BIRTH.WEIGHT.cut)
frequency.table <-transform(BIRTH.WEIGHT.freq)
frequency.table## BIRTH.WEIGHT.cut Freq
## 1 (0,500] 1
## 2 (500,1e+03] 5
## 3 (1e+03,1.5e+03] 1
## 4 (1.5e+03,2e+03] 12
## 5 (2e+03,2.5e+03] 19
## 6 (2.5e+03,3e+03] 50
## 7 (3e+03,3.5e+03] 75
## 8 (3.5e+03,4e+03] 33
## 9 (4e+03,4.5e+03] 7
## 10 (4.5e+03,5e+03] 2Create a histogram of birth weights for girls’ data subset using breaks and hist command.
breaks<-seq(0,5000,by=500)
hist(BIRTH.WEIGHT, xlab = "Birth Weight in [grams]", ylab="Frequency",ylim=c(0,80),main="Distribution of Birth Weights for Girls", col="pink",border="blue")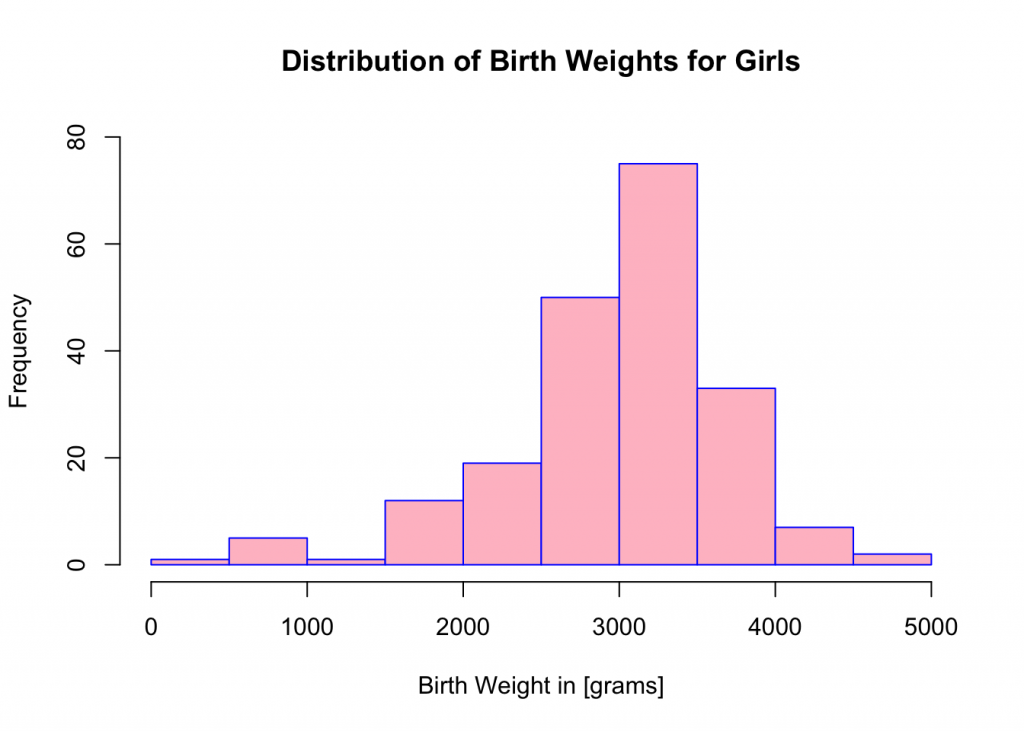
detach(girlD)Now: Select all rows from BirthsD data set that pertain to boys’ births and include all variables, (columns).
Start by naming this subset boyD, (boys’ data).
boyD <-BirthsD[GENDER..1.M. == "1", ]
attach(boyD)## The following objects are masked from BirthsD:
##
## ADMITTED, BIRTH.WEIGHT, DISCHARGED, FACILITY, GENDER..1.M.,
## INSURANCE, LENGTH.OF.STAY, TOTAL.CHARGEShead(boyD,3)## FACILITY INSURANCE GENDER..1.M.
## 2 Albany Medical Center Hospital Blue Cross 1
## 4 Albany Medical Center Hospital Insurance Company 1
## 5 Albany Medical Center Hospital Insurance Company 1
## LENGTH.OF.STAY ADMITTED DISCHARGED BIRTH.WEIGHT TOTAL.CHARGES
## 2 2 FRI SUN 3900 3632.5
## 4 5 MON SAT 2800 8536.5
## 5 2 FRI SUN 3700 3632.5summary(BIRTH.WEIGHT)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 300 2900 3400 3273 3650 4900Create a frequency table for Boys’ birth weights.
BIRTH.WEIGHT.cut <-cut(BIRTH.WEIGHT,breaks)
BIRTH.WEIGHT.freq <-table(BIRTH.WEIGHT.cut)
transform(BIRTH.WEIGHT.freq)## BIRTH.WEIGHT.cut Freq
## 1 (0,500] 1
## 2 (500,1e+03] 2
## 3 (1e+03,1.5e+03] 2
## 4 (1.5e+03,2e+03] 5
## 5 (2e+03,2.5e+03] 8
## 6 (2.5e+03,3e+03] 39
## 7 (3e+03,3.5e+03] 69
## 8 (3.5e+03,4e+03] 57
## 9 (4e+03,4.5e+03] 10
## 10 (4.5e+03,5e+03] 2Create a histogram of birth weights for boys data subset using breaks and hist command.
breaks<-seq(0,5000,by=500)
hist(BIRTH.WEIGHT, xlab = "Birth Weight in [grams]", ylab="Frequency",ylim=c(0,80),main="Distribution of Birth Weights for Boys", col="blue",border="yellow")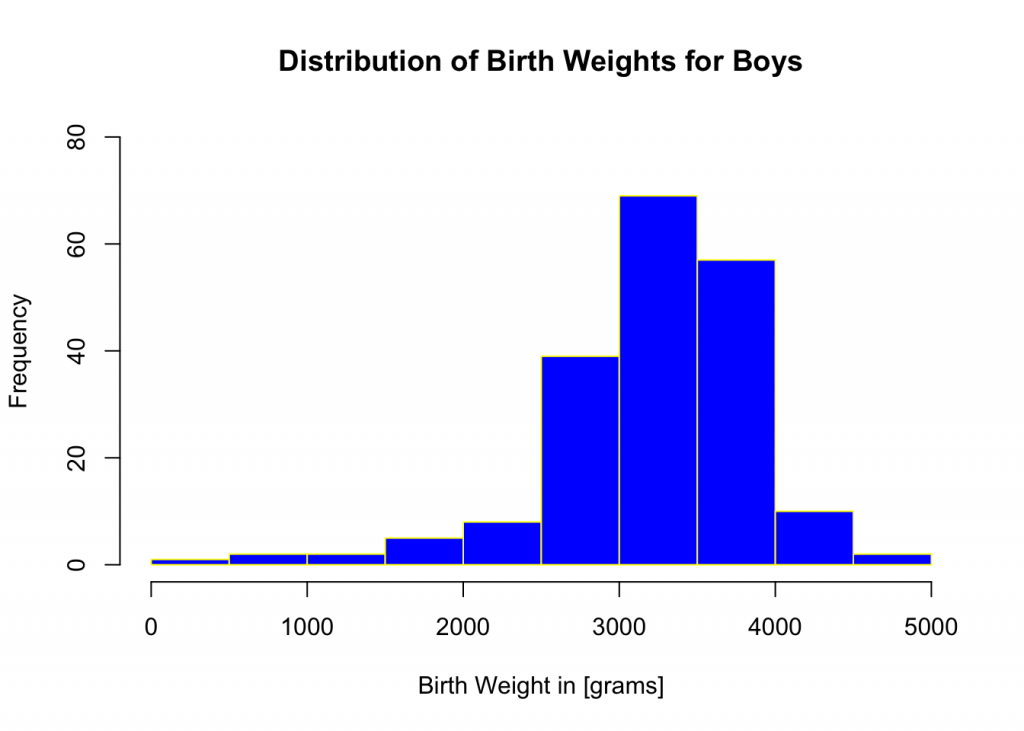
detach(boyD)Extra Credit Assignment
1. Use parts of the above syntax and create two box-and-whisker plots, (one for each gender), describe variability in each subset, and compare variability between genders.
2. Write a report using any word-processing program. Use full and complete sentences; remember to include numerical and graphical summaries in your report. In addition, attach R printout with input/output.
- Data Set 4: extracted from M. F Triola, Essentials of Statistics Sixth Edition, Pearson↩
Recent Comments